

Inmos Technical note 36
1 Introduction 2 Flight simulators 3 Architecture
3.1 An overview
4 Implementation
4.1 The ring Control process The ringController The simulation process The main process 4.2 The Data Base manager Building the BSP tree Traversing the BSP tree 4.3 The transformation process 4.4 Clipping 4.5 Shading 4.6 The display 4.7 User interface 4.8 The hardware implementation
5 Conclusions
6 References
72 TCH 036 01
Parts of this note are to be published by The International Supercomputing Institute, Inc. (ISI, Inc.) in the proceedings of the 3rd International Conference of Supercomputing and, as such, are copyright of ISI Inc.




A transputer based multi-user flight simulator
Recently, one of the most popular applications for computer graphics has surely been simulation systems, for example flight simulators. The aim of these systems is to generate some scenario in sufficient detail, and with enough realism to give the operator the impression that the exercise is happening in the real world, and not in a simulated one.
Systems like these require huge amounts of computation, and very high performance display systems to achieve such realism. In fact, most current systems are implemented in hardware to get the supercomputer performance required. The major attraction with these systems is the interaction the user has with the environment (flight simulators allow the pilots to push their aircraft to their limits, without endangering themselves (and others)). The biggest setback is their inability to allow the environment to react with the user (the computer can rotate radar dishes etc., but complex movements like other aircraft cannot be done without huge amounts of extra processing).
This technical note describes the implementation of a multi-user flight simulator system using transputers and occam. The design allows any number of single-user simulators, each a small supercomputer in its own right, to be linked together to allow interaction between systems. By having a number of other pilots controlling the other objects in the simulation, a trainee pilot can be subjected to more complex scenarios than those that could be programmed into a computer.
The program described is written entirely in occam, and the hardware used in the implementation consists of a number of transputer variants (T212, T414, and T800), all running on standard INMOS transputer evaluation boards. These boards are connected using the INMOS links, allowing complex systems like this to built with relative ease (approximately 10 minutes to wire up a four player implementation of the simulator).
More details of the transputer and occam can be found in [1],[6] The joystick module is the only custom hardware used. This board is described in the user interface section of this note.
Simulators (for aircraft, cars etc.) are becoming increasingly popular applications for computer graphics. Top of the range flight simulators can be used to train pilots for any situations that might occur (freak weather conditions, instrumentation failure, surprise ambush from mischievous mountain ranges, slight reduction in the number of wings etc.), without endangering pilot, passenger, or crew.
A simulator system must be able to portray the outside world in sufficient detail (both graphically on the windshield, and numerically using instruments), and possibly simulate the motion of the vehicle using a motion platform, such that the pilot feels that he/she is really flying the aircraft. Such a system consists of a number of very high performance sub-systems, such as a display system, motion controller, and a data base system that can maintain a model of the world (and any objects that may appear in it), and enviroment data (rain, clouds, etc.) that must be accessed during the simulation. All this data must be displayed fast (and realistically) enough to give the impression of real flight. To get a frame rate of 20 to 30 frames per second, most of the work is currently done in hardware, which explains the high cost of this sort of system.
With a multi-user simulator, each node must be able to access the data and display it in accordance to the current position of the craft at that node. Also needed is a knowledge of where all other users in the system are, so they can also be displayed (if visible).
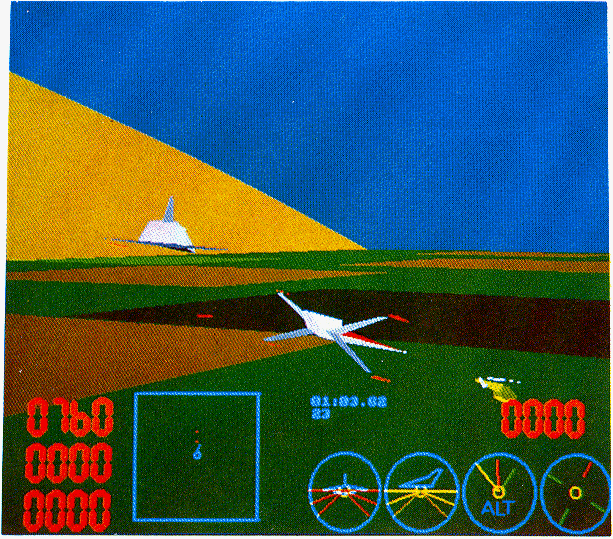
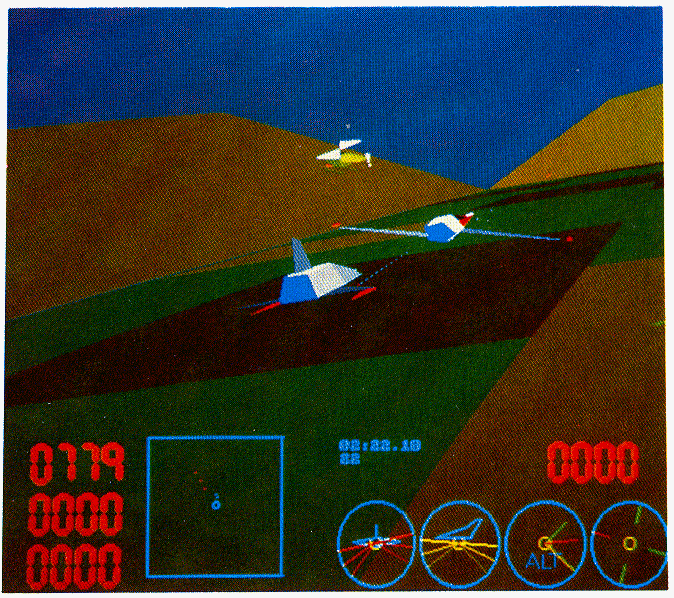
This implementation of a flight simulator allows any number of users, each with their own simulation engine, to interact. Each user gets a view of the world as if looking through the cockpit window. The world is made of polygons, and these are displayed at a rate of approximately 17 frames per second (at about 200 polygons per frame).
This frame rate is limited by the design of the graphics board used in the current system. To avoid visual artifacts it is neccessary to wait for frame fly-back before updating the display. As there are only two display banks on the IMS B007 graphics board, this has the effect of holding up link communications with the shader processors for up to one frame time (1/50th sec). If the wait for frame fly back is removed, the frame update rate is increased to approximately 22 frames/sec, as the buffered image can be displayed as soon as it is received. An enhanced graphics board is currently being designed at INMOS, which has up to four frame buffers, allowing higher frame rates (as the n+1th frame can be read whilst the nth frame is waiting to be displayed) WITH frame fly back.
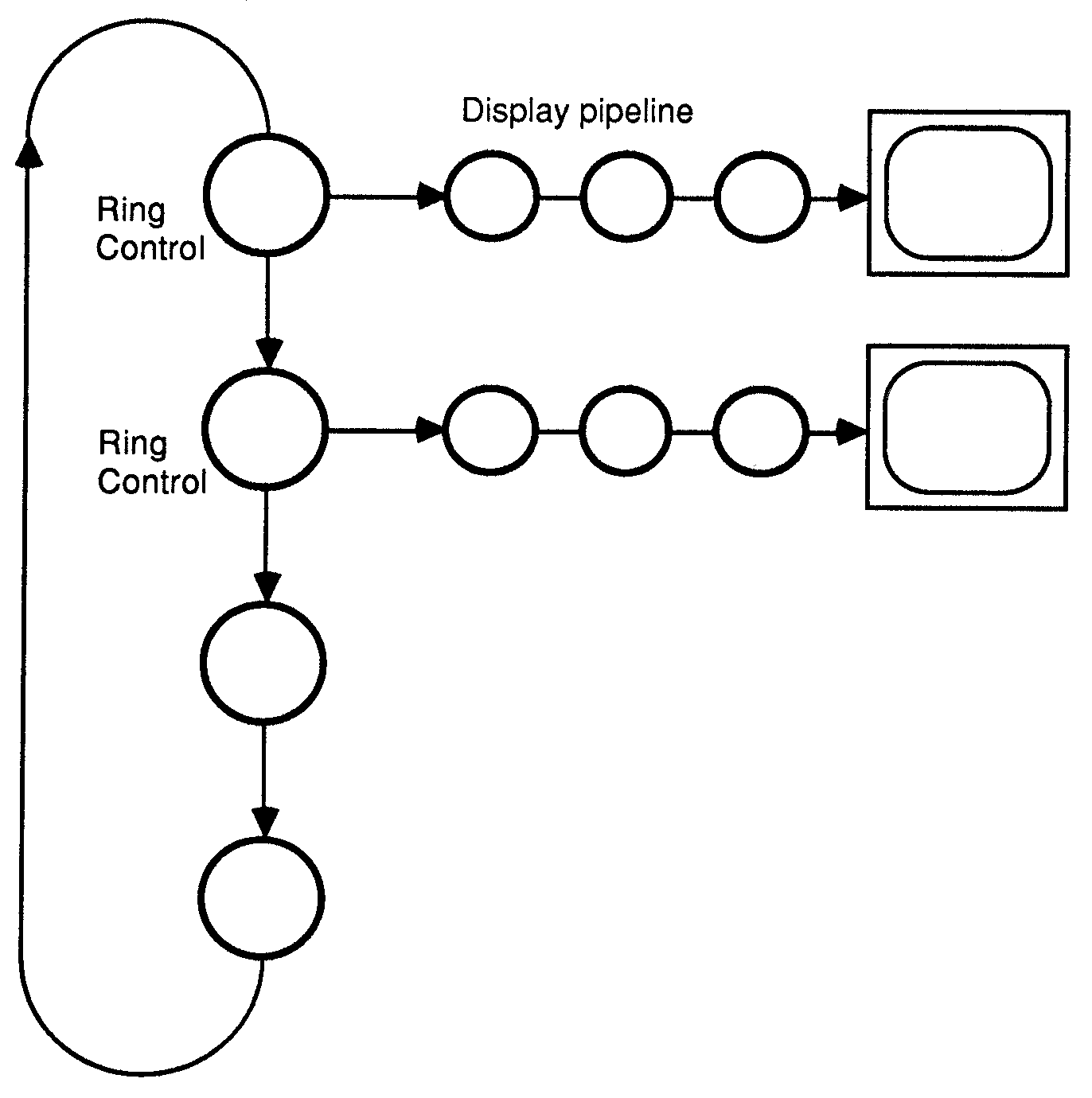
All users are connected in a ring. Any part of the world that needs to be distributed is passed around to each user in turn, who can read it, modify it, or ignore it, then pass it on to the next user. Objects can be dynamically added to this network (such as missiles that have been fired), and taken out when finished with, The ring architecture allows any number of users to be included in the system, and the software has been written with this feature in mind.
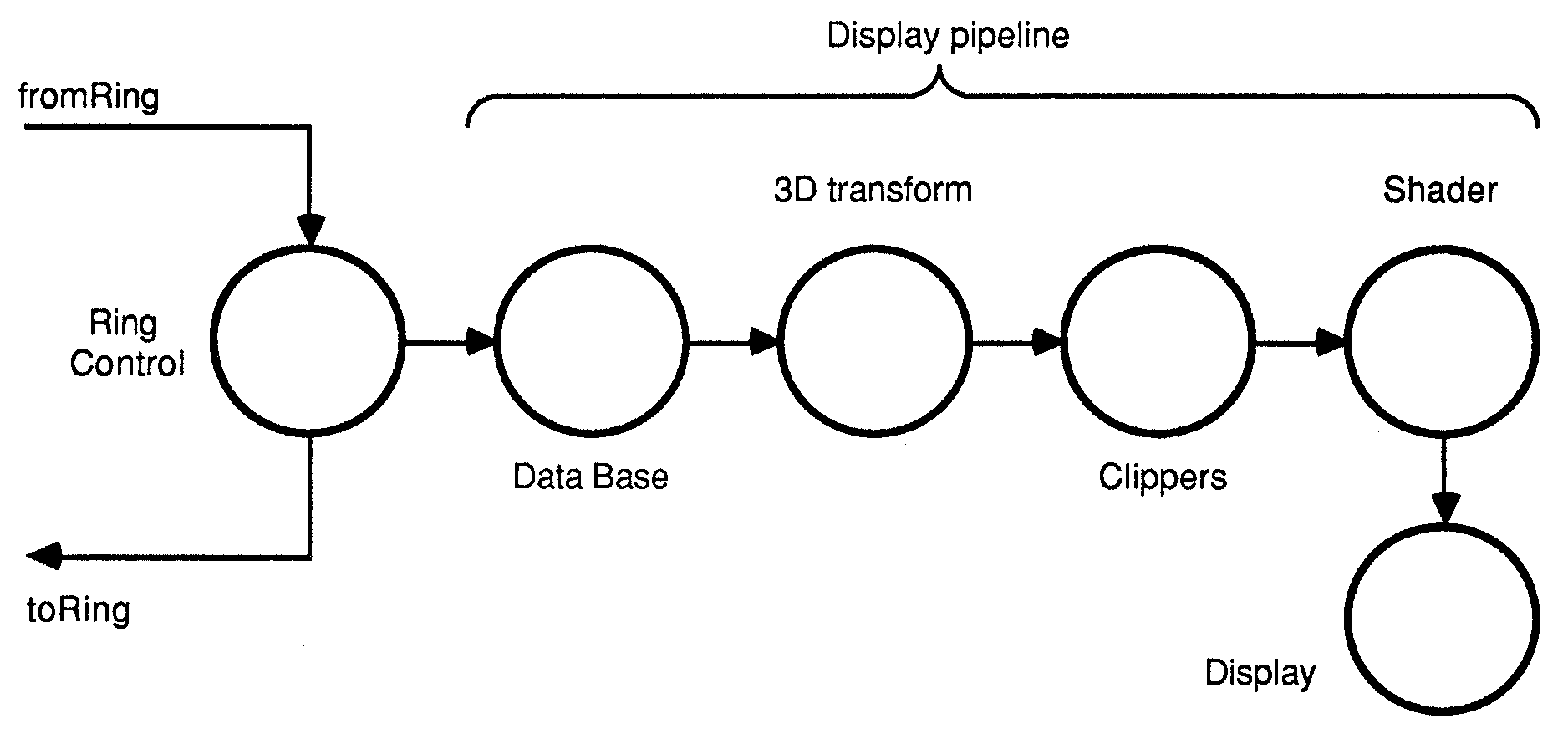
The architecture for a single user system is shown in figure 1. The system has been sub-divided into the most logical processes that occur in a simulator, e.g. the core simulator, 3D transformation, clipping etc. Note that this is the software model for such a system, and not the hardware implementation, which is described in the hardware implementation section.
Figure 1: Architecture for one player
Before explaining in detail the various processes that are used in the simulator, a brief overview of the system, and some of the terminology used, is required.
The system has been designed to allow any number of flight simulators, such as the one shown on figure 1, to be connected in a ring. Messages are passed around the ring defining the position, orientation of objects in the simulation. Figure 2 shows an example of four such systems connected in a ring.
Figure 2: The ring architecture
The ring Control process handles all ring communications, and interaction with the pilot controls. From these information sources, a description of the next visible scene for this user can be derived.
Objects are described as a set of polygons, and these polygons are stored in a large data base. To display an object, these polygons must be output such that the near faces of the object obscure those further away. The data base process takes care of this hidden surface algorithm.
The polygons described in the data base are not suitable to be:written directly to the screen. Each polygon must undergo a transformation to convert it to a displayable form. In the following sections, reference will be made to model, world, eye and screen co-ordinate systems. Figure 3 shows an example of how these different co-ordinate systems relate. Converting between co-ordinate systems requires the co-ordinates (of a polygon, for example) to be transformed using matrix multiplications [4], [5). The transformations can be rotations about an axis, scaling, and translation along an axis. For example, the transform from model to world space requires a 90 degree rotation about the Y-model axis (see Fig.3).
Figure 3: The coordinate systems
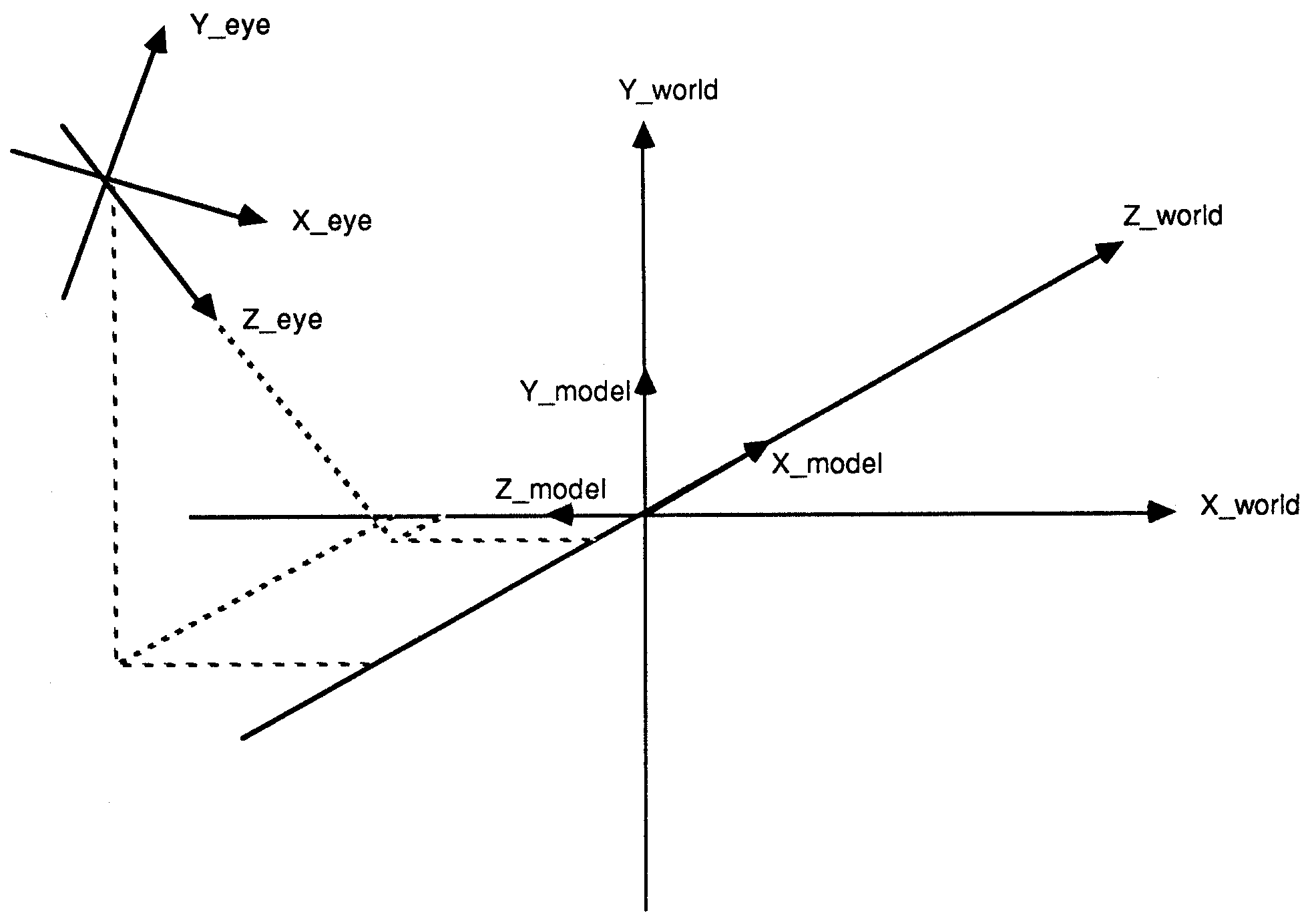
Matrices may be concatenated, allowing a single point to undergo a number of transformations with only a single matrix multiplication. The order in which the transformations are applied to a point is determined by the order in which the transformation matrices are concatenated. By reversing this order, a reverse transformation (from screen to model co-ordinate systems, for example) can be generated.
The conversion from model to screen co-ordinate systems is performed by the transformation process. Matrices that define the transformations to be performed are generated by the ring Control process, and are used to transform the polygons that are output from the data base.
Before shading a polygon, a clipping operation must be performed to remove any parts of that polygon thlat may not be visible. As well as clipping to the screen boundaries, the polygons must also be clipped to the z co-ordinate viewing boundaries (often referred to as the ‘hither’ and ‘yon’ clipping planes) to remove parts of polygons that may be behind the viewer, or beyond the horizon. Before clipping to the screen boundaries, the perspective calculations are performed. This effectively scales the 2D polygons according to their distance from the view point.
Many shading algorithms can be used to generate the final display. The simplest is flat shading, where each polygon is filled with a designated colour. More complex shading algorithms take the position of light sources into account, and so require more complex calculations to be performed at each pixel to determine the colour and intensity at that point. Shadows, highlights and reflections could also be included, but require vast amounts of extra processing.
In the following sections, an understanding of both occam and the transputer is assumed.
The ring Control process controls the operations on all data on the ring. Fig.4. shows the internal configuration of this process.
Figure 4: The ring controller
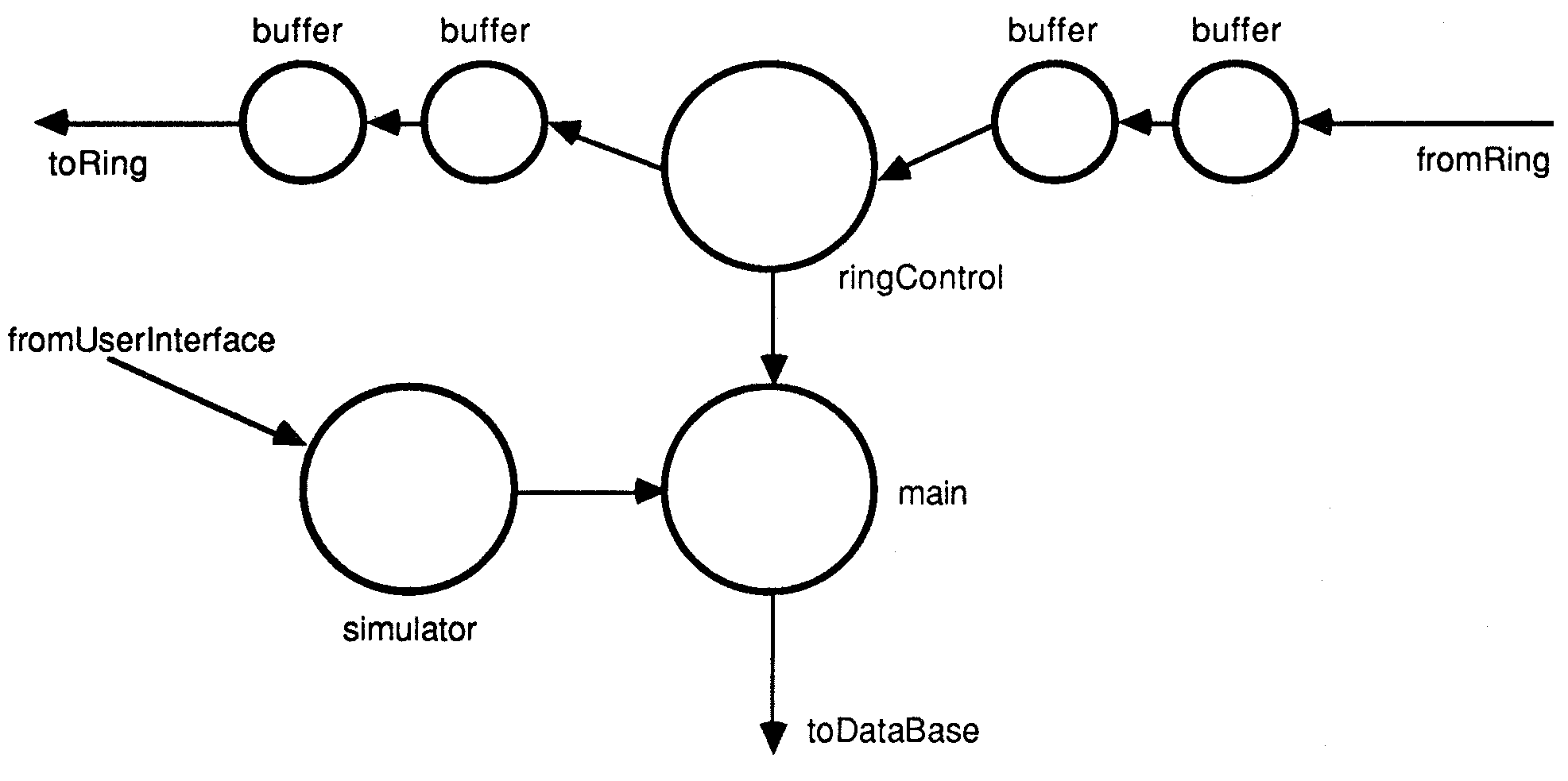
The ringController
The interplayer communications are implemented as a ring based architecture. This allows any number of users to be incorporated into the system.
For a true multi-user system, each single user simulator must have access to the same data base. As shared memory is not supported, the systems must communicate by passing messages over occam channels [6]. The data base required for a simple flight simulator is quite large, and passing this as a message between many small flight simulators would severely limit the performance of a system. One feature with such a system that can be exploited is that a very small proportion of the data base actually changes during the operation of the simulator. The ground remains static, buildings tend not to move very often, and so the communications can be reduced to passing information regarding dynamic objects within the system, i.e. the aircraft controlled by the other users.
Messages passed around the ring are object descriptors (such as type, position, and other attributes). By keeping the descriptor as a block, the transfers of the block around the ring can be done ‘for free’ by the block move engines in the transputer links. Double buffering techniques (described in [7]) increase system performance by allowing the processing of the current descriptor whilst outputting the previous one and inputting the next.
The ringController process (and associated buffers) handle all ring traffic. The buffers allow the number of messages on the ring to change dynamically (deadlocks could occur if all links used in the ring were active (busy transmitting or receiving), and a new object (such as a missile) was added).
A number of simple decisions are made on the objects as the ringController receives them. These are
[blockSize]INT inBlock, outBlock :
SEQ
in ? inBlock
WHILE running
SEQ
IF
opponent_aircraft
PAR
toMain ! inBlock
outBlock := inBlock -- (1)
missile
SEQ
toMain ! inBlock
fromMain ? outBlock -- (2)
owners_aircraft
SEQ
toMain ! inBlock
fromMain ? outBlock -- (3)
PAR
in ? inBlock
out ! outBlock
1 The descriptor is sent to the main process, and can be also be passed on to the ring.
2 The result from the main process could be the missile attributes being altered to indicate the opponents missile has hit this (the testing process) aircraft, or the missile has been removed from the ring (in which case, the output to the ring is not performed).
3 The result is the new owner descriptor (current position etc.).
The simulation process
The simulation process controls the interaction with the player (via a joystick interface), and adjusts the position and rotation of objects belonging to that player (such as missiles and the aircraft the player is flying). There are up to three objects to keep track of (one aircraft and two missiles), and any of these can be under control of the player. The others fly ‘blind' (i.e. along the course on which they were fired). When a missile is under control, the aircraft continues flying in the direction it was moving before the missile was taken under control.
SEQ
... get data from user interface
... decode to give any changes in direction etc
IF
driving_missile
... alter missile course, move others
TRUE
... alter aircraft course, move others -- (1)
... get status from main -- (2)
IF
collision -- (2)
... change state to explode
TRUE
SKIP
PAR
... output the player descriptor
... set up head-up display (HUD) -- (3)
... send HUD (also marks end of frame)
1 Each object is stored as current position and delta movement for the next frame. When controlling a certain object via the joystick interface, the stored delta values are overwritten with those derived from the joystick inputs. Here, any environment simulations, such as gravity and atmospheric conditions such as wind, can also be included.
Transformation matrices are generated to describe the positions and orientation of these objects, and the view point, and these matrices are passed to the main process.
2 The main process (see below) will, at this point, have completed the reading of data from the ring, and will have a list of objects for output, together with information giving the result of the collision detection, and an array of coordinates to be used in the map. This data is taken as being a request for the object descriptor generated in (1).
The value of the collision tag is used to alter the object attributes to signal an explosion (which selects an explosion data base to be displayed). During the explosion cycle, inputs from the user are ignored, and the aircraft is forced into a fixed sequence of moves before restarting. The co-ordinate array passed is used in the head-up display.
3 The head-up display is sent as a set of high level commands to the display engine. The attitude of the aircraft (pitch, roll, yaw etc.) is converted to a sequence of line draw commands (which build up an artificial horizon display), the map is a set of plot pixels commands, and the instruments are defined as circle commands. These commands are built into a display list, which is transfered as a single block through the display pipeline to the display process.
Missile descriptors pass around the ring until the missile has hit something (either another aircraft or the ground), or has run out of fuel. The ‘hit’ detection is done in the main process below, and that process will request a particlar missile be updated or removed from the ring. The current implementation allows for up to two missiles per person to be active (flying) at any time. This is limited only by the available ring bandwidth. Future topologies should allow for more objects to be present in the system.
The main process
The main process (the frame generator) takes its inputs from the ringController and simulation processes, and calculates which of the objects can be seen. The information from the simulation process determines the location (in world space) of the player’s screen, and this information is used to translate all other objects to the eye_space of the player.
Any objects that can be seen are z-sorted to give a list of object descriptors, which are output (in reverse depth order) to the pipeline to be converted into polygons and shaded. At this stage, only a description of the object (e.g. type, location, rotation) is needed. It is expanded on in later stages of the pipe.
Within the 2-sort routine, collision detection and trivial rejection are also performed. As there is no master in the system, all user processes do their own collision detection (i.e. they detect if they have been hit). If a hit has occurred, messages are passed back around the ring to the owner of the other object in the collision, who will take the appropriate action.
Both collision detection and trivial rejection are done using bounding boxes, which undergo a simple transformation to put the bounding box in eye space. If the bounding box can be clipped from view, the object is rejected (and is not inserted in the list). If two bounding boxes intersect, a collision has occurred, and the other object owner is informed that a collision has taken place. Because all players do their own collision detection, a test of all boxes interacting with all other boxes does not have to be performed. The test is simply sort each object as it arrives from the ring, and test the closest object with the bounding box of the player. As the test is done when the descriptor is read from the ringController process, the hit flag can be set in the object attributes before it is sent back to the ring.
The end of a frame is signalled by the mai,n process reading the object descriptor of its owner from the ring (this is sent out at the start of the frame, and its return signals that all other descriptors have passed through). At this point, the list of descriptors is sent to the traverser process (in reverse z order) for the hidden surface algorithm to be executed.
SEQ
PAR
... get ring data, x-sort, collision detect -- [1]
... output head-up display, ground -- [2]
PAR
... output sorted descriptor list -- [3]
... get new player data from movement process -- [4]
1 For each item received from the ring, do a trivial reject and collision detect (if the object is closest to the player), and set hit flag if collision has occurred. If the object belongs to this player (i.e. a missile), then request the new missile descriptor from the simulation process. The descriptor is sent back to the ringController to be inserted into the ring.
2 Whilst reading in the next frame data, we can keep the display pipeline busy by sending the head-up display list to the graphics engine, followed by the end of frame marker, and then getting the traverser to output the ground details for the next frame.
3 For each object in the list, three items must be passed to the display pipeline. First, the transformation matrix (from model to screen space, including perspective transform), is passed on to the transform process. The view point (which is transformed to be in the model co-ordinate system) is passed to the traversed process, as is the model type. The last two items are used to select and output a particular portion of the data base.
4 Pass the map data (and result of the collision detection) to the movement process, and receive the descriptor for next frame.
The models that are used in the simulator are stored as a tree of polygons. A version of the Binary Space Partitioning (BSP) algorithm [2] is used to determine which polygons are visible (and in what order) from any view point.
The algorithm is quite simple. A polygon lies on a plane, defined by the equation
Ax+ By+ Cx + D = 0
where A, B, C, D are constants (calculated from three co-planar vertices of the parent polygon). If a point [x,y,z] satisfies the above equation, that point is said to lie on on that plane. However, if the result is negative, the point is said to lie behind the plane, and if the result is positive, the point lies in front of the plane.
BSP trees store the polygons in a recursive manner, with a polygon at each node of a binary tree. Each node points to a sub-tree of polygons that lie in front of the parent polygon, and a sub-tree of polygons the lie behind the parent.
Building the BSP tree
Building the BSP tree is a recursive operation. Starting with a list of the polygons that make up a model, we set the root node of the tree to be the first polygon in the list. The plane on which this root node lies is calculated (the A, B, C, D constants are stored in the record for that node, for use during the tree traversal at run time), and all subsequent polygons in the list are tested to see whether they lie in front or behind the root node.
After testing all polygons in the main list, the in front and behind pointers of the root then point to two sub-lists of polygons. Each sub-list is then recurswely traversed, until a binary tree, with a single polygon per node, is created.
The test to derive whether a polygon lies in front or behind the plane involves entering each polygon vertex into the plane equation. If all vertices lie in front of the plane, the polygon is in front of the plane, and it is added to the end of the in_front sub-list of the root. If the polygon lies behind, it is added to the behind sub-list (when the plane and the polygon are co-planar, the polygon can be added to either list). Note that if the polygon is split by the plane (some vertices are in front, some are behind), the polygon must be divided into two sub-polygons, which are inserted into either sub-list.
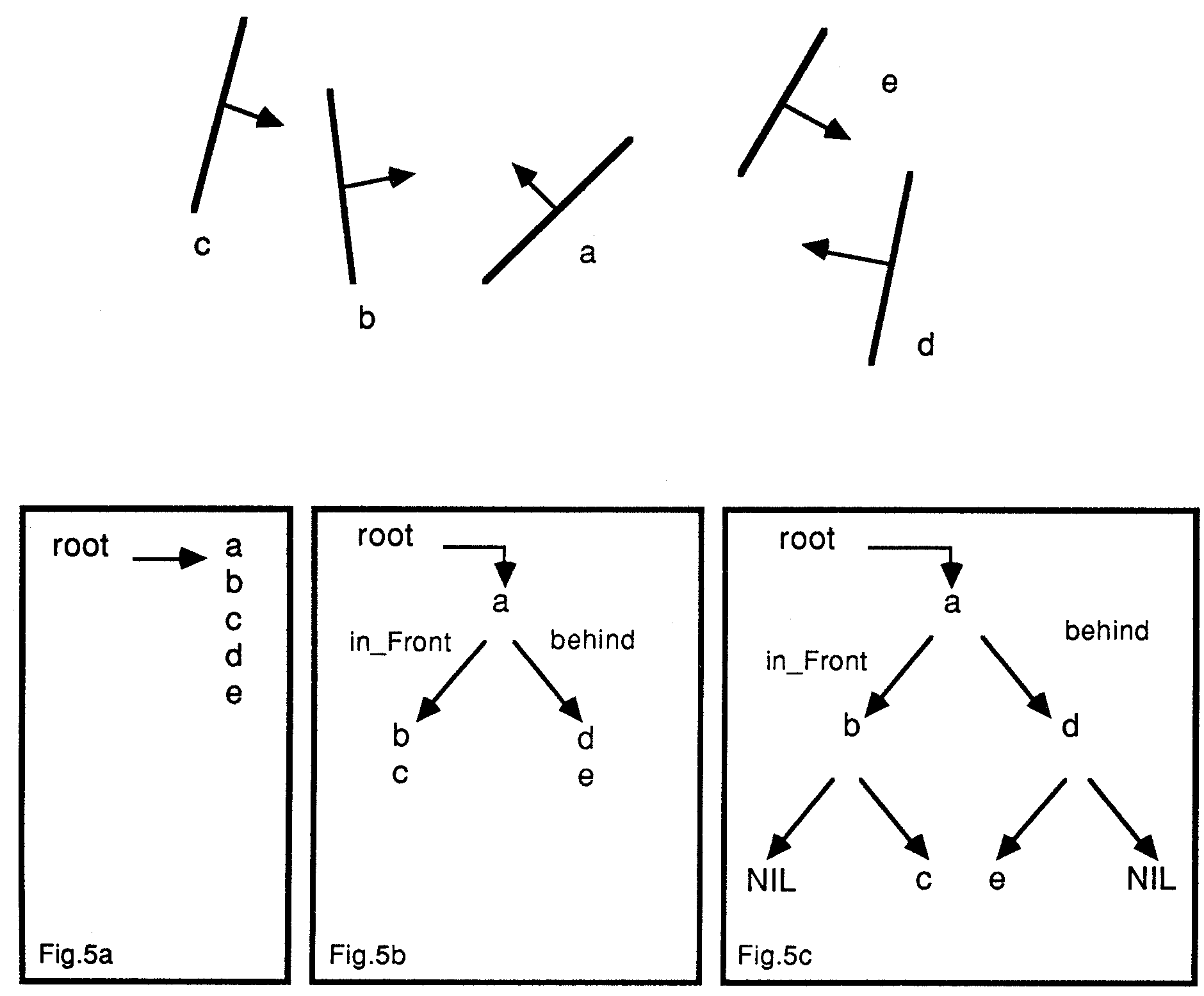
A graphical example is shown in Figure 5 (for simplicity, we will work in two dimensions, but it is simple to extend the principles to three dimensions). At the start (5a), the list contains five polygons a, b, c, d, e (the arrows are used to show where in_front is for each polygon). Polygon a is chosen to be the root, and Figure 5b shows the result of the tests performed on the other four polygons. If the algorithm traverses the in_front sub-list, then the behind sub-list (as done by the combine routine in the description below), Figures 5c shows the results as each sub list is traversed.
Figure 5: Building a binary space partitioned tree
Here is a piece of pseudo-code describing the algorithm [2].
PROC make_tree (poly_list)
returns (BSP_tree) ;
if (poly_list is EMPTY)
return (NULL_tree)
else
{
root := select (poly_list)
back_list := NULL ;
front_list := NULL ;
foreach (polygon in poly_list)
if (polygon is not the root)
{
if (polygon in front of root)
Addlist (polygon, front_list) ;
else if (polygon is behind root)
Addlist (polygon, back_list) ;
else
{
splitpoly (polygon, root, frontpart, backpart) ;
Addlist (frontpart, front_list) ;
Addlist (backpart, back_list ) ;
}
}
return (combine_tree (make_tree (front_list)), root, (make_tree (back_list )) ) ;
}
END
combine_tree links the root to the sub trees.
This procedure will generate a BSP tree from a list of polygons. The node chosen for the root strongly determines the order in which the polygons are stored in the tree. In the simulator, it was necessary to have certain polygons at leaf nodes of the model tree, and so tree was constructed manually. This is not an easy task, but a writing a routine to build the tree, following certain constraints as to the location of arbitrary polygons, was not thought possible in the time allowed.
The BSP trees are static for all the models, and so can be constructed during the initialisation phase of the the simulator.
Traversing the BSP tree
Traversing the tree is a recursive operation. Here is a piece of pseudo-code describing the algorithm.
traverseTree (tree)
if (tree is empty) return
else
{
if (view point in front of root polygon)
{
traverseTree ( tree -> back )
displayPolygon ( tree -> rootPolygon )
traverseTree ( tree -> front )
}
else
{
traverseTree ( tree -> front )
displayPolygon ( tree -> rootPolygon )
traverseTree ( tree -> back )
}
}
The result of this operation is the polygons in the tree always displayed in a back to front order, i.e. the furthest polygon from the view point is output first. In this way, the correct hidden surface solution is achieved for all possible view points.
A state machine is required to simulate this recursive operation when using occam. The state machine has two variables, the current node in the tree, and the current action being performed. Nodes and actions are stacked as the state machine traverses the tree.
push (NIL, a.terminate)
action := a.testPosition
node := rootNode
WHILE action <> a.terminate
IF
action = a.tsstPosition
IF
node = NIL
pop (node, action)
inFront (node, viewPoint)
SEQ
push (node, a.traverseFront)
node := tree [ node + backSubTree]
TRUE
SEQ
push (node, a.traverseBack)
node := tree [ node + frontSubTree]
action = a.traverseFront
SEQ
outputPoly (node)
action := a.testPosition
node := tree [ node + frontSubTree]
action = a.traverseBack
SEQ
outputPoly (node) -- [1]
action := a.testPosition
node := tree [ node + backSubTree]
1 In some cases, it is not neccessary to draw this node, as the definition of being ‘behind’ a polygon means the polygon is facing away from the viewer, and so should be obscured by polygons facing the viewer. For example, a cube has six faces, but it is only possible to see a maximum of three. The other three are back facing polygons. These back facing polygons need not be drawn.
For space considerations, we have a boolean tag in the record for each polygon which enables ‘back face rejection’ on specific polygons. Wings of an aircraft can be described as a single polygon, displayed no matter where the the view point is, but the box defining the bulk of an aircraft body can be forced to reject back facing polygons.
To output a model, the traverser process reads a view point and model type from the main process (above). The model type selects the particular tree to be output, the view point determining the order the polygons are output.
The transformation process takes polygons (lists of points), and transforms these points from the model co-ordinate system to the screen co-ordinates
3-Dimensional transformation (scaling, translation and rotation) is performed using matrix multiplication [4]. Matrix multiplication can be implemented very efficiently on the T800 (see [5] for a more detailed discussion). Whilst the FPU is calculating the product (for example) of two matrix elements, the integer processor can be calculating the address where the result must be stored. By overlapping the floating point calculations with the index calculations (done by the compiler, incidentally), a co-ordinate transform
[4] REAL32 a, c [4] [4] REAL32 transform .. .. SEQ matrixMult (c, a, transform) -- does (c := a * transform)
can be done in approximately 19 microseconds. This gives a peak transform rate of over 52,000 points per second.
The transformation process accepts a transformation matrix from the pipeline. All subsequent polygons are then tranformed with that matrix until a new matrix is received.
Before the polygons can be displayed, they must be clipped to the viewing boundaries. Clipping in the z-plane removes the parts of polygons that are behind the view point, and also polygons that are beyond the horizon. Perspective calculations are then performed (scaling the polygons with respect to their distance from the view-point). Finally, the polygons are clipped to the screen boundaries.
Both the z-clip and perspective calculations require floating point calculations. However, the screen is ad-dressed as an integer device, and so the x and y-clip operations can be performed in integer form. This eliminates the need for a more expensive floating point unit in the later clipping stages.
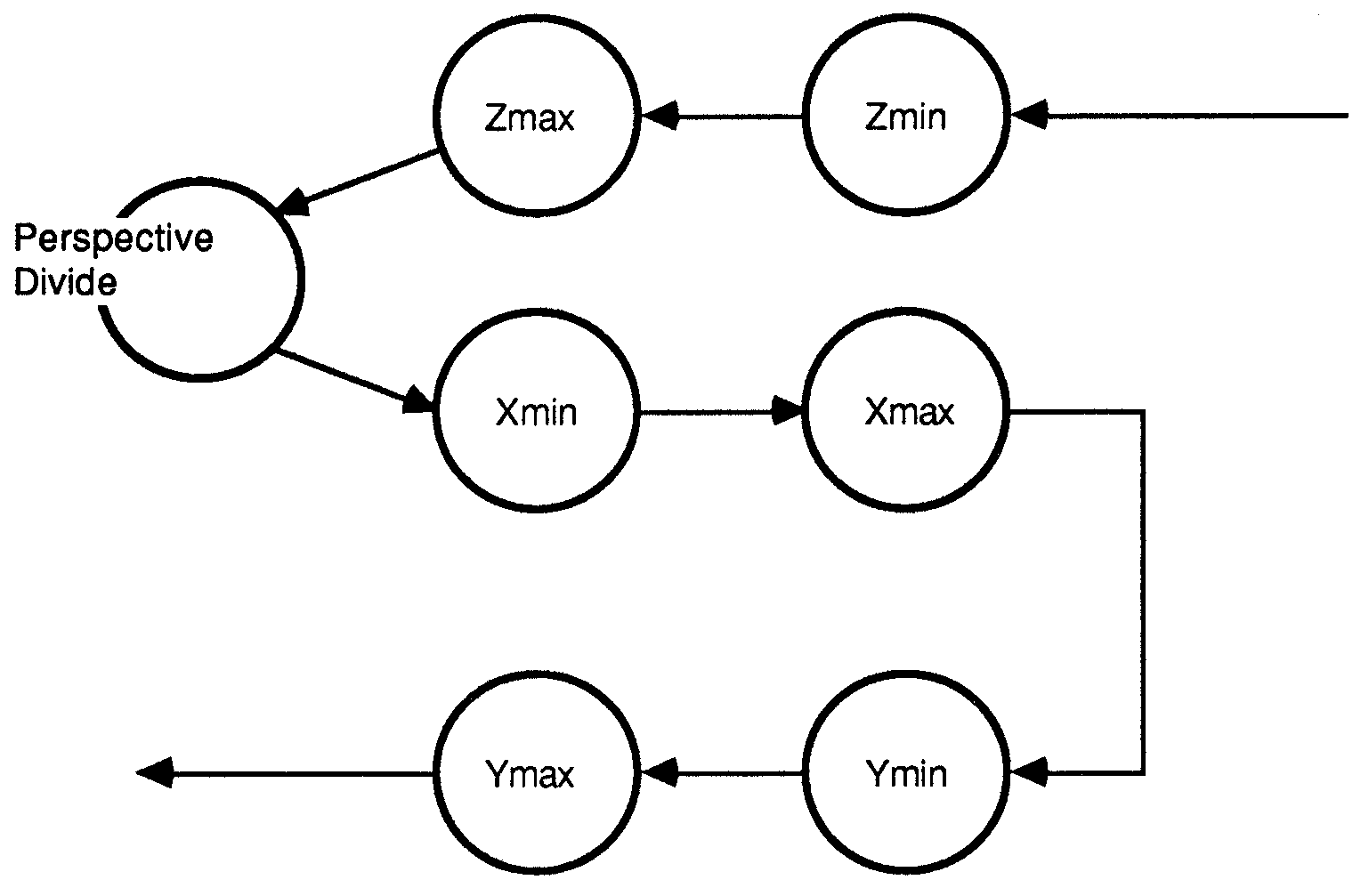
Fig.6. shows the structure of the clipping processes. The output of the final y-clipper is a stream of polygons ready to be drawn on the screen.
Figure 6: The x,y,z clipping architecture
For the polygon filling, the screen is split into a number of sub-screens, each handled by its own shader (Fig.7. shows the internal structure of one such shader). In the current implementation, there are four sub-screens, each handled by a transputer. Each polygon that survives the clipping process is passed to all shading processors, which shade their part of the polygon.
Figure 7: Internal structure of shader
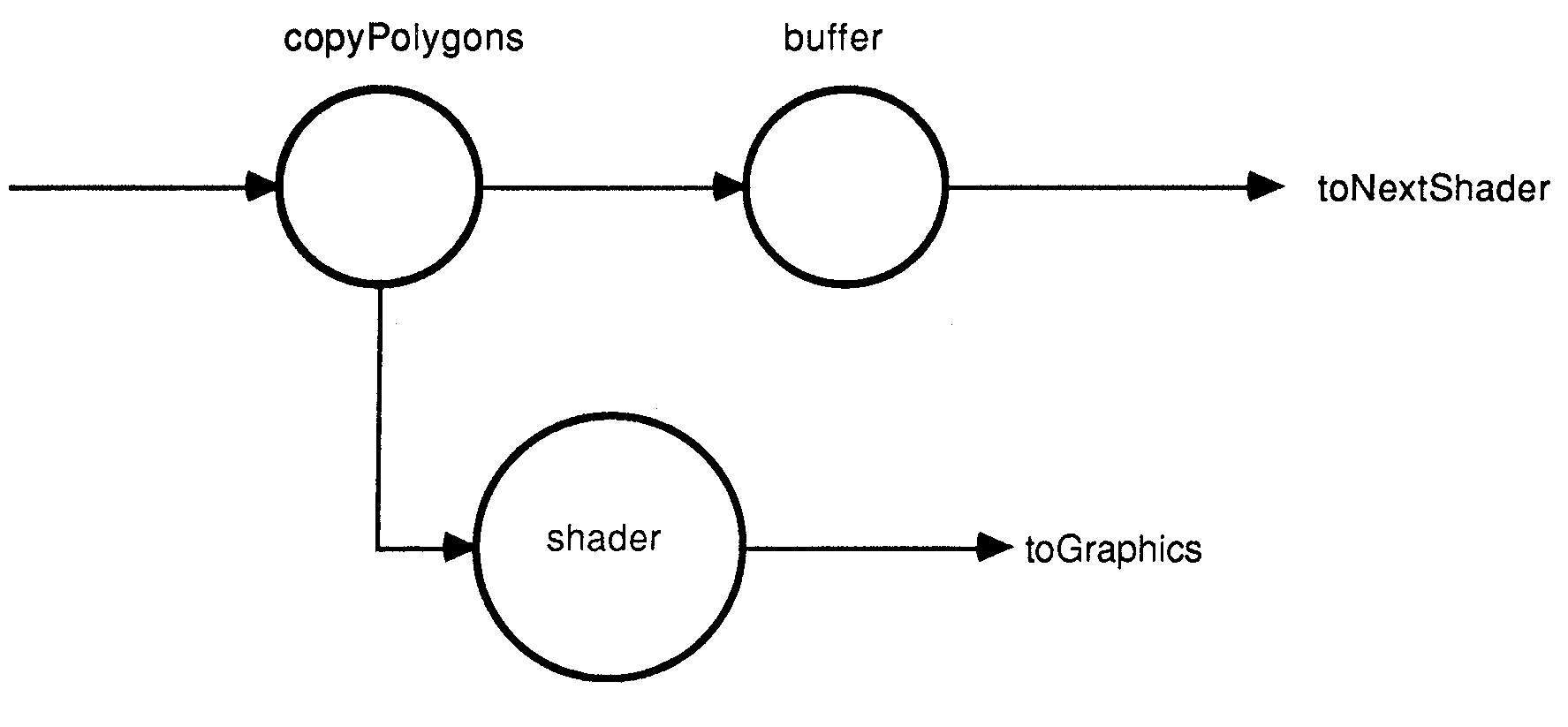
Each polygon shading process shades every fourth line of the polygon. The operation starts at the bottom vertex (smallest y co-ordinate) of the polygon. Here, two vectors are set up, which define the rate of climb along the two edges which meet at that vertex. This vector defines the step in x that will occur for every step in y. The y step is four pixels (for four shading processors). After initialising these vectors, shading is a matter of taking a step in y, calculating the new (x,y) locations for along the edges, then joining those points with a horizontal line (the colour of which is defined in the polygon descriptor). As each of the polygon vertices are encountered, the vector defining the appropriate x step is recalculated.
Polygons are flat shaded (for simplicity). Shading the horizontal line is simply a matter of block moving data from on-chip RAM into the buffer used to generate the sub-screen. As the shading processor may see many lines within one polygon, an array (stored in the on-chip RAM) is initialised to the polygon colour as the polygon is read in, and this is used for every line fill until a new polygon is received.
When implemented on a T414-20 with single wait-state external memory (200 nanosecond cycle), a single shader can fill polygons at a rate of 16 million pixels (8 bits per pixel) per second, or 62 nanoseconds per pixel. Therefore, four shading processors can shade at a rate of 64 million pixels per second, only 15.6 nanoseconds per pixel. If more performance is required, more shading processors can be added.
At the end of each frame, the sub-screen is transferred to the graphics process for display. Again, full use of double buffering of the links and processor is used, to allow the last frame’s worth of image to be transmitted to the display engine, while the start of the next frame is being computed. The output format is simply the y co-ordinate of each line, followed by the 512 bytes that make up that line. The 512 byte line is transferred as a single block, increasing efficiency.
The display card (Fig.8.) accepts complete sub-screens from the shader processes, and transfers them (using the Inmos links) directly into screen RAM.
Figure 8: The display process
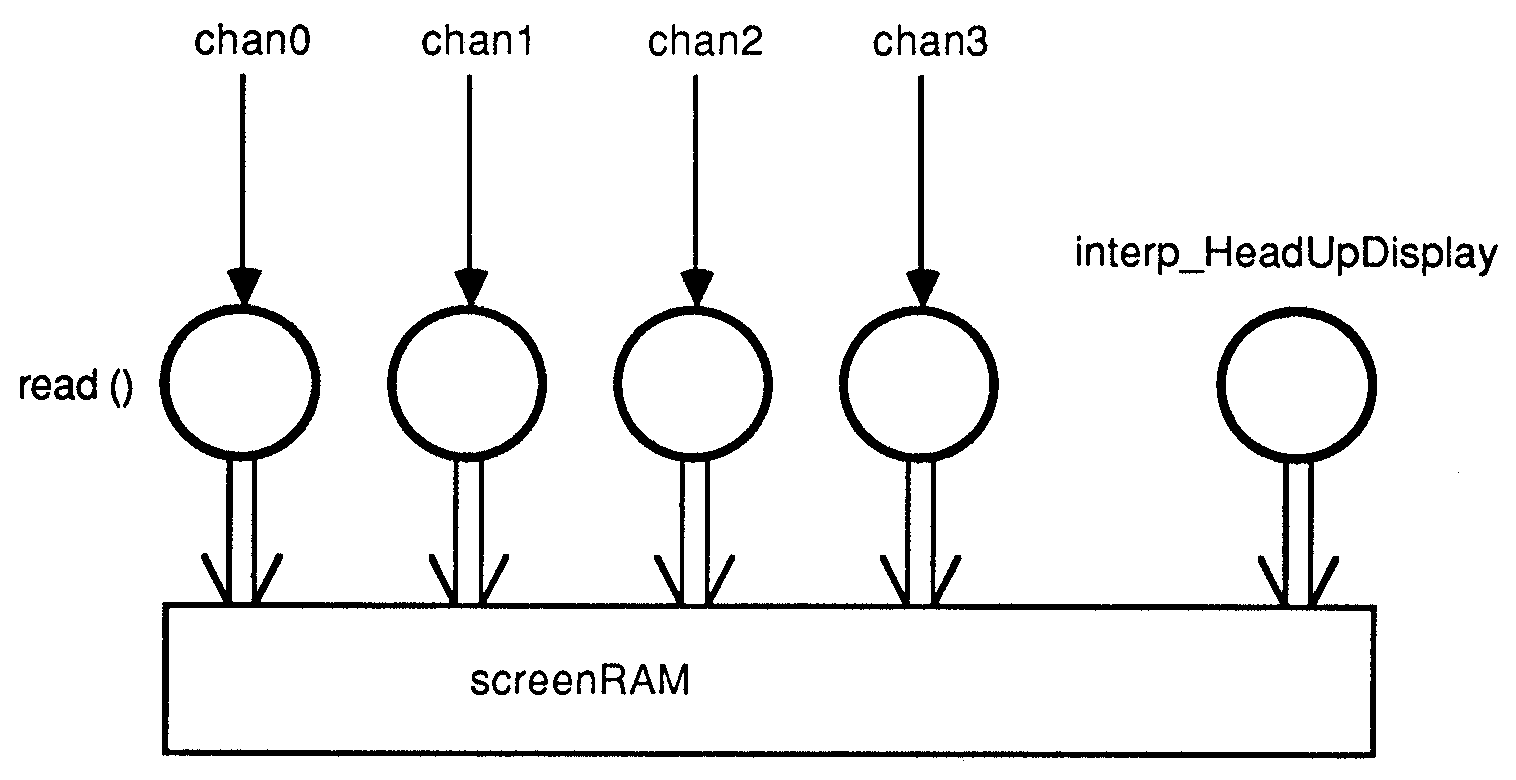
The graphics card (IMS B007 transputer evaluation board) used has a single IMS T800, thus giving four links into the display process. The four input channels chan0, 1, 2, 3 are mapped onto the hardware links, allowing complete sub-screen to be read directly into the screen RAM independent of the processor. Hardware double buffering on the IMS B007 allows one screen of data to be read in while another screen is being displayed, so screen update is invisible. At the end of frame mark, the screens are flipped over.
Also passed at the end of frame is extra information which is used to generate a head-up display (for the next frame). This information can be processed while the next frame data is being read in.
PLACE chan0 AT link0in :
PLACE chanl AT linklin :
PLACE chan2 AT link2in :
PLACE chan3 AT link3in :
WHILE running
SEQ
in ? headUpDisplay
... input bottom_128_1ines
PRI PAR
... input top_384_1ines -- at high priority
interp_HeadUpDisplay() -- using bottom 128 lines
flipScreens
The data from the polygon shaders is input from all four links simultaneously.
PRI PAR
{{{ input top_384_1ines
PAR
read (chanO) -- read from link0
read (chan1)
read (chan2)
read (chan3)
}}}
interp_HeadUpDisplay ()
The read processes are started at highest priority, and will be descheduled as each link starts to operate. Once all high priority processes have been descheduled, the processor, is free to run the low priority interp_HeadUpDisplay process. These processes can be run in parallel, as there are effectively operating on two seperate arrays, i.e. the bottom 128 lines and the top 384 lines of the screen.
The head-up display information is written to the screen using the extra graphics instructions [3] of the IMS T800. The move2Dnonzero command will transfer all 'non-zero' bytes of an array, giving the effect of an overlay operation.
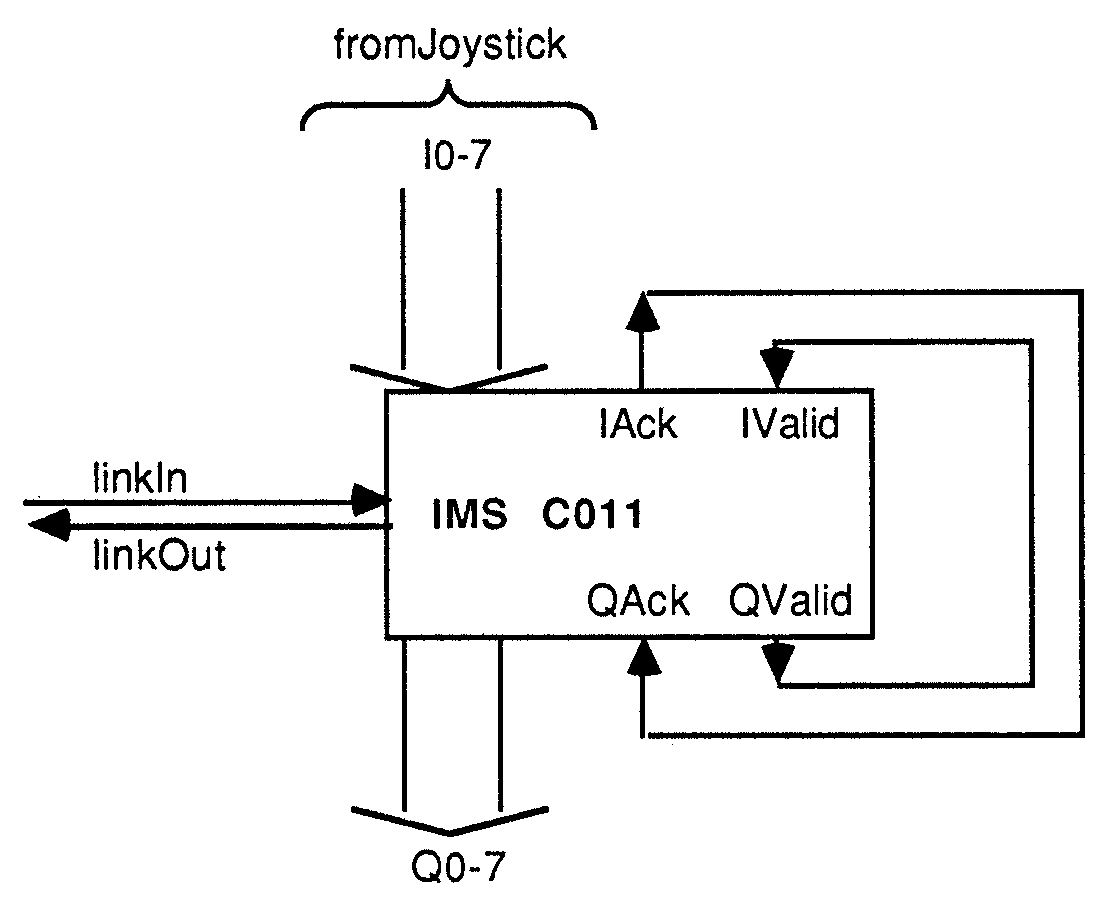
The interface to the user joysticks is implemented using IMS C011 link adaptors. These devices convert byte wide parallel data to the Inmos Link format, and vica versa.
The joysticks used simply present 6 bits of information to the link adaptor. This device is wired such that a message byte, sent from the controlling transputer, will trigger the input half of the C011 to sample, and transmit the current joystick value. This value is decoded to find which switches were active at that time. A circuit diagram for the joystick interface is shown in Fig.9.
Figure 9: The joystick interface module
The hardware used in the demonstration system is shown in Fig.10., along with the mapping of the processes described above.
Figure 10: Hardware implementation for a single user system
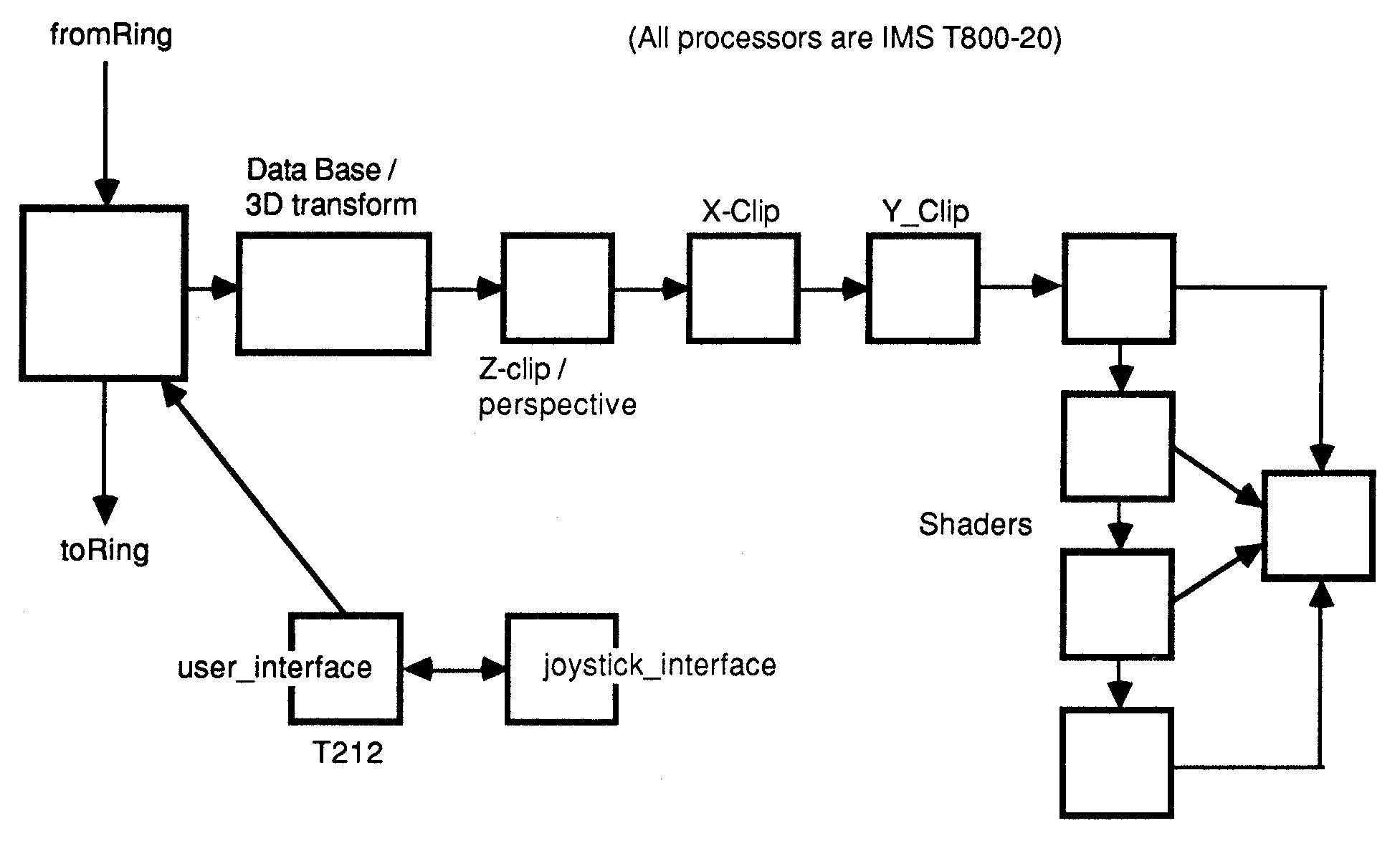
The front end of the system (the ring controller and transforming processes) are floating-point intensive, and are PLACED onto IMS T800 processors. Other processes, such as the x and y-clippers do not use the FPU of the IMS T800, but take advantage of the higher link bandwidth available (all links are run at 20 MBits per second, and use overlapped acknowledge packets).
As well as interfacing to the joystick modules, the IMS T212 processors run an autopilot process, which cuts in if the joysticks are not touched for a certain time.
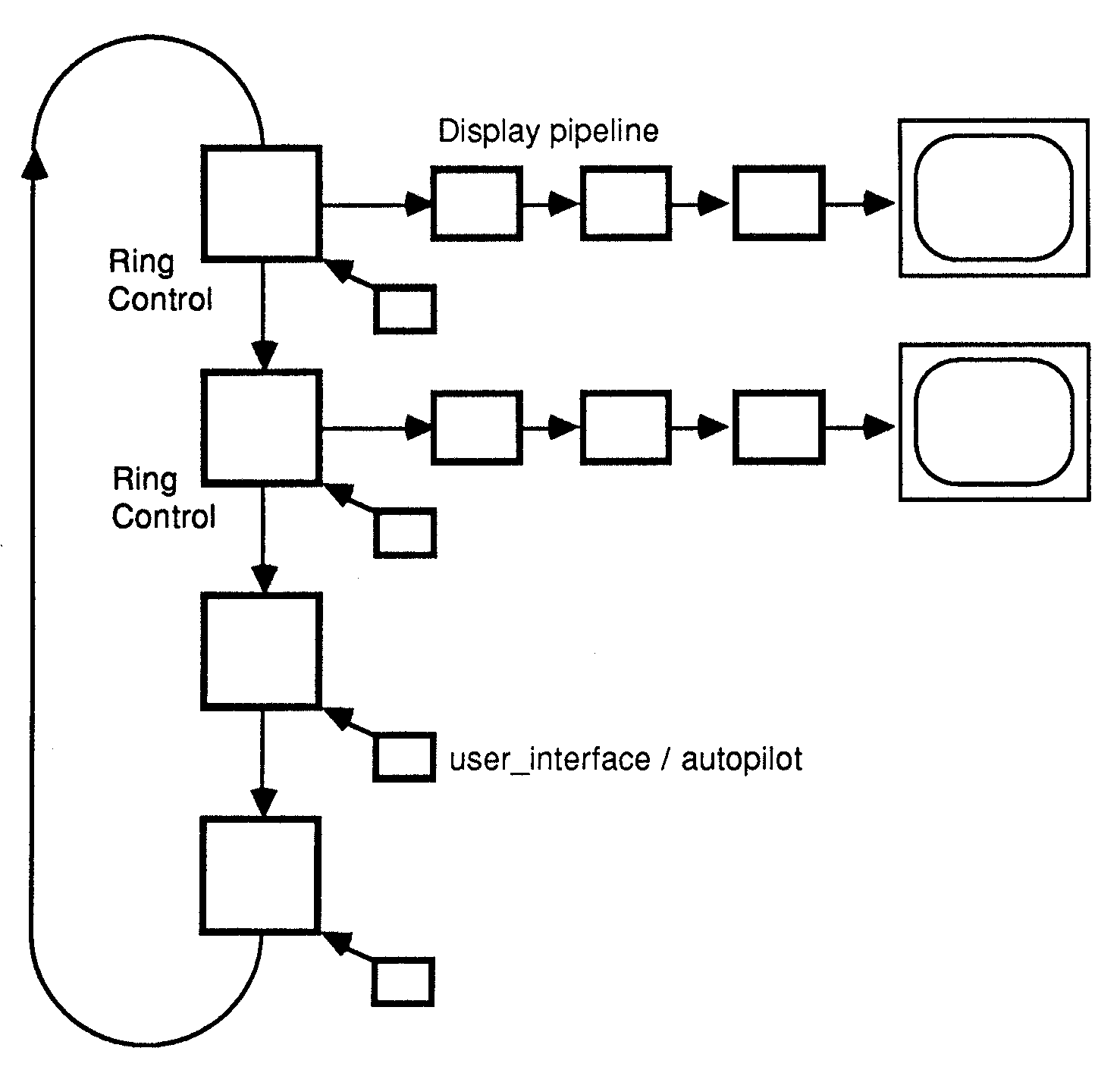
The minimum hardware for a system is a single user simulator as shown in Fig.10. Larger systems can consist of a mixture of these full simulators, and a cut down version with no display pipeline, connected in a ring (see Fig.11.). The cut down simulator runs an aircraft under autopilot control, giving the interactive users something to shoot at!
Figure 11: A two player, two autopilot example
Described is an implementation of a multi-user, interactive flight simulator, using occam and transputers. The system hardware is standard Inmos transputer evaluation boards, and all the software (written using the Inmos transputer development system) was written in under three weeks. We believe this is a record for such a system.
Included at the front of the note are some photographs which show a number of frames taken from the display during a typical combat. The stills do not do justice to the system, which really comes alive when sitting in the pilot seat!
Future upgrades to the system include 3D terrain mapping, better shading models, more realistic flight characteristics. As extra features are added, more transputers can be added into the system to cope with the extra processing required.
Acknowledgements
Thanks to Phil Atkin for his amazing polygon shader (and his re-write of my BSP traverser), and for getting the simulator to appear at SIGGRAPH 87, where it stole the show.
Also, thanks to Pete Highton for his ideas and support during the development of the simulator just before the T800 launch.
[1] The transputer architecture reference manual
INMOS Ltd
Bristol
[2] Near Real-Time Shaded Display of Rigid Objects
Henry Fuchs, Gregory D. Abram, Eric D. Grant
Computer Graphics (Vol 17, No 3)
July 1983
[3] Notes on Graphics Support and Performance
Improvements on the IMS T800
Guy Harriman
Technical Note 26
INMOS Ltd,
Bristol
[4] Principals of interactive computer graphics
William M. Newman and Robert F. Sproull
McGraw Hill
[5] High performance graphics with the IMS T800
P. Atkin and J. Packer
Technical Note 37
Inmos Ltd
Bristol
[6] occam reference manual
INMOS Ltd
Bristol
[7] Performance Maximisation
Phil Atkin
Technical Note 17
INMOS Ltd
Bristol